مفهومِ اندازهگیری در نظریه کوانتوم
The concept of measurment1in QT
فشرده
درک و بیان پدیدهها با یاری مفهومها امکانپذیر است. مفهومها از کنش و واکنشهای ما با محیط حاصل میشوند. درجه و سطح آگاهی ما از دنیائی که در آن زندگی میکنیم رابطهی مستقیم با دامنه و عمق مفهومهائی دارد که در طول تاریخ کسب نمودهایم. به عبارت دیگر، ما واقعیتهای خارج از حیطهی مفهومها، توان فیزیولوژکی (ساختاری، حواس) و دستگاه ادراکمان (تابع پروسه تکامل و بطرز طبیعی مشروط و محدود۲) را به سختی و اغلب تنها با یاری ابزار، یعنی با واسطه درمییابیم. عرصهی خاص و بارز چنان واقعیتهائی از جمله پدیدههای کوانتومی هستند. بهعنوان مثال، برای ما تصور اینکه یک ذره میتواند همزمان در مکانهای مختلف باشد اگر نه محال حداقل اما بسیار دشوار است. از اینرو ما مایلیم آن را یک فانتازی، یک برداشت غلط بدانیم. غافل از آنکه چنان پدیدهای واقعیت دارد و به اثبات رسیده است. ابزار ما در دستیابی به این نوع شناختهای فووقالعاده، علم و تکنیکِ است. مثال ذکر شده نشان میدهد که برای بیان و توضیح پدیدههای کوانتومی نیاز به مفهومهای خاصی، مانند مفهوم ناهمدوسی۳، است. به عبارت دیگر، با مفهومهای صرفا کلاسیک (که در اصل میباید همهی آنها را مفهومهای شبه کوانتومی تلقی کنیم) نمیتوان پدیدههای کوانتومی و مسائل حل نشده مانند گرانشِ کوانتومیِ، سیاهچالهها و یا مِهبانگ را درک و بیان داریم.
یک مثال عملی ساده معروف به آزمایش دو شکاف۳:
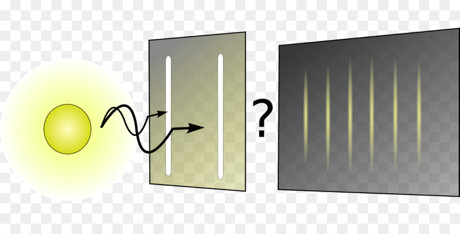
زمانیکه ما یک ذرهی کوانتومی مانند فوتون یا الکترون را بسوی دوشکاف گسیل میداریم (تصویر۱) نتیجه، برخلاف دیدگاه کلاسیکی ما که ذره از یکی از دو شکاف خواهد گذشت، چنان است که گوئی ذره از هر دو شکاف گذشته است! این نتیجه بههیچ شکلی با تجارب و مفاهیم دنیای کلایسک ما همخوانی ندارد. اما صحت و واقعیت دارد، به اثبات رسیده است و ما میتوانیم آن را برخلاف تصور و باورمان (پیش از آزمایش) به عین مشاهده کنیم. نتیجهِ آزمایش واقعی و غیرقابل انکار است. اما علت آن چیست و چگونه میتوان آن را مستدل نمود؟
پاسخ به این پرسشها خواهان توجه به کنش و واکنش میان ذرهی متعلق به دنیای کوانتوم در لحظهی برخورد با شئای از دنیای کلاسیک بهعنوان محیط یا ابزارِ اندازهگیری و ارائه مفهومهائی با توان بیان مشاهدات و نتایجِ شگفتانگیزِ کوانتومیِ است. البته ممکن است ما فکر کنیم مشکلی با مفهوم اندازهگیری نداریم و قرنهاست که با آن آشنا هستیم. اما لزوما چنان نیست و حتی عکس آن صادق است و اشتباه میکنیم، اشتباهی که فیزیکدانان نامداری نیز مرتکب شدند. اصلاح این اشتباه که با بنیادیترین مسائل فیزیک و معرفتشناسی رابطهی مستقیم دارد از نیمهی دوم قرن بیستم آغاز شده است!
در این مقاله میکوشم ابتدا مفهوم اندازهگیری را برای دو حالت توضیح دهم (پیشگفتار) و در ادامه به مفهوم اندازهگیری در نظریه کوانتوم که از مرتبه، جایگاه خاص و اهمیت بسیار بالائی در شناختِ ما از واقعیتها۴ دارد بهپردازم.
پیشگفتار
اندازهگیری به فعالیتی برنامهریزی شده برای تعیین مشخصهِ یک شئای، رویدادی یا کمیتی در مقایسه با اشیاء، رویدادهای دیگر و یا با واحدِ کمیتِ مربوطه گفته میشود، فعالیتی که میتواند بهشکل مستقیم یا غیرمستقیم باشد. در حالت اول شئ مورد اندازهگیری، برای مثال طول یا عرض یک سااختمان، از طریق قراردادن واحد طول در کنار ساختمان مستقیما قابل تعیین، اندازهگیری، است. در حالت دوم، ارتفاع ساختمان، را میتوان غیرمستقیم از طریق روابط هندسه مثلثات تعیین نمود. مثالی دیگر: طیف و طولِ موجِ نورِ عناصرِ شیمیائی را میتوان در آزمایشگاه تولید و سنجید. با بهرهگیری از این اطلاعات و تجزیه طیفِ نورِ ساطع شده از خورشید و یا ستارگان دیگر میتوان از طریق مقایسهی آنها با یافتههای آزمایشگاهی به عناصری که در خورشید و ستارگان وجود دارند پیبرد.
اندازهگیری را میتوان از نظر مفهومی به دو بخش یا سطح تقسیم نمود: مفهومِ کلاسیکیِ اندازهگیری و مفهومِ کوانتومیِ اندازهگیری. مهمترین فرقِ این دو باهم به نقشِ مفهومِ احتمال در آنها برمیگردد. در مفهومِ کلاسیکی تصور ما براین است که ارزشِ اندازهگیری (Messwert, measured value) پیش از اندازهگیری تعریف شده است، امکان اندازهگیری دقیق وجود دارد و تکرار آن همواره به نتیجهی یکسانی میانجامد (البته با ملاحظهی دو خطای به اصطلاح قابل چشمپوشیِ سنجشگر و سیستمِ اندازهگیری). یعنی، برای این حالت مفهومِ احتمال معنا و نقش تعیین کننده ندارد. اما درست عکس این حالت را ما در اندازهگیریهای کوانتومی شاهد هستیم. به این معنا که در اینجا همواره صحبت از احتمالات است. یعنی، مفهوم احتمال در دنیای کوانتوم تعیین کننده و جزو ذات آن محسوب میشود. اما به چه دلیل ما اندازهگیری در دنیای کلاسیک را که از مواد و مصالح کوانتومی (اتمها) بنا شده فارغ از مفهومِ احتمال تصور میکنیم؟ بهنظرم به ۴ دلیل:
۱ـ باور به امکانِ اندازهگیری دقیق. این باور ریشه در تصورِ ما از پیوسته بودن کمیتهای فیزیکی دارد، ۲ـ اُنس گرفتن، عادت کردن، به اندازهگیری در محدودههای بزرگتر از اندازه اتمها در طول قرنهای متوالی، ۳ـ حِسِ بینیازی به دقتِ بیشتر از حد لازم برای رفع نیازها و ۴ـ تاثیرِ ناچیز (قابلِ اغماض) ابزارِ اندازهگیری و سنجشگر بر شئ مورد بررسی.
نکات ذکر شده ذهنیتی را در ما ایجاد کرده که باورمان شده است مشکل خاصی با مفهومِ اندازهگیری نداریم. یعنی، ما فکر میکنیم که قادریم کمیتها را تا هر قدر که لازم است دقیق و حتی صد در صد دقیق اندازهگیری کنیم.۵
اما از اوایل قرن بیستم عامل مهم و غیرقابل انکاری در عرصه شناخت از طبیعت ظاهر گشته که سخت مفهوم شناخته شدهی ما از اندازهگیری را زیر سؤال برده است. اینکه معلوم شده کمیتهای فیزیکی نه بهشکل پیوسطه بلکه ناپیوسطه، گسسته، هستند. اندازهگیری کمیتهای گسسته اما ما را با مشکلات فراوانی مواجه میکند. به این علت که ما در اینجا با ابعادی در محدودهی اتمها سر و کار داریم که بسیار حساس نسبت به کوچکترین کنش (تاثیر) هستند. برای بررسی این نوع اجسام نیاز به ابزاری است که تاثیرشان بر آنها قابلِ اغماض باشد تا بتوان آنها را کمابیش آنگونه که هستند ملاحظه نمود. آیا چنین چیزی امکانپذیر است؟ آیا امکان دارد جسمی را که تاثیر ابزار بر آن در محدودهی تاثیر متقابل جسم بر ابزار است بدون هیچ تغییری مشاهده نمود؟ آیا در یک چنین وضعیتی بدور از تصور است که شاهد درهمتنیدگی ذره و ابزار و تغییر حالت هر دوی آنها باشیم؟ و در نتیجه نتوانیم جسم (ذره) مورد بررسی را آنگونه که هست ملاحظه کنیم؟
تاثیر ابزارِ اندازهگیری بر حالتِ شئ در دنیای کلاسیک را میتوان با ملاحظهی عوامل چهارگانهی ذکر شده ناچیز شمرد. اما آیا میتوان این شیوه را بیهیچ دغدغهای به محدودهی اتمها و ذرات مادون اتمها (به دنیای کوانتوم) نیز بسط داد؟ بیشک خیر! چراکه در اینجا تاثیرِ ابزارِ اندازهگیری بر شئِ مورد بررسی قابلِ اغماض نیست.
اندازهگیریِ اجسام کوانتومی به خاطرِ تاثیرپذیریشان از کوچکترین تاثیراتِ سیستمِ اندازهگیری از یک طرف و تاثیرگذاری همان اجسام بر سیستمِ اندازهگیری از طرف دیگر (بهخاطر ظرافت و حساسیتی که میباید داشته باشند) منجر به تغییراتی در هر دو سیستم میگردد. به این معنا که کنش و واکنش میان آن دو سبب درهمتنیدگی و تغییراتِ بازگشتناپذیرِ حالتِ هر دو سیستم میشود. بههمین علت ما قادر نیستیم یک جسمِ کوانتومی را آنگونه که واقعاً هست ملاحظه کنیم! البته در اینباره میانِ فیزیکدانها و فیلسوفانِ طبیعی اختلاف نظر وجود دارد که بیشتر مربوط به مسئله و مفهوم اندازهگیری میشود.
مفهومِ اندازهگیریِ کوانتومی و مفهومِ ناهمدوسی از مفهومهای بنیادیِ علم فیزیک محسوب میشوند. این دو مفهوم در دهههای اخیر مورد توجه خاص قرارگرفته و پژوهش در بارهی آنها رو به افزایش است. بههمین خاطر لازم میدانم در زیر توضیحاتی را در رابطه با مفهومِ اندازهگیری در حیطهِ نظریه کوانتوم ارائه کنم (مفهومِ ناهمدوسی را پیشتر در مقاله جداگانه توضیح دادهام۳). لزومِ شناخت از دو مفهومِ نامبرده بهویژه از آنجا ناشی میشود که بدانیم سطح و عمقِ علومِ طبیعی و معرفتشناسیِ فلسفیِ مدرن ما رابطه مستقیم با واقعیتهائی (واقعیتهای کوانتومی) دارد که از ملاحظهی این دو مفهوم بدست میآیند. (توضیحِ مفهومِ واقعیتِ کوانتومی در مقالهام تحتِ عنوانِ: مفهومِ واقعیت در نظریه کوانتوم۴)
اندازهگیریِ کوانتومی
در سال ۱۹۰۰ ماکس پلانک در اثرِ مهم و تاریخی خود در توضیحِ شدتِ تابشِ حرارتیِ اجسامِ سیاه از ضریبی (کمیتی) معروف شده به ثابتِ پلانک h (انرژی ضرب در زمان با واحد ژول ثانیه Js برای h) بهره میجوید که مقدارِ آن برابر با Js ۳۴–۱۰×۶،۶۲۶ میباشد (توجه شود به کوچکی این کمیت!). ثابتِ پلانک از مفاهیمِ اساسی در نظریه کوانتوم و رابط میان انرژیE به فرکانسِ f (بسامد) امواج است. برای مثال انرژی یک فوتون برابر است با ثابتِ پلانک ضرب در فرکانس فوتون (E = hf ). ثابتِ پلانک کوچکترین مقداری است که میتوان برای حاصلضرب انرژی و زمان تصور کرد.۶ در واقع این ضریب نشان میدهد که نظریه کوانتوم در چه مقیاسی معتبر است. چنانچه بتوان در اندازهگیریها ناثیر h را نادیده گرفت (h => 0) در اینصورت اندازهگیری در حوزهی کلاسیکی قرار دارد، یعنی در ابعادی بزرگتر از محدودهی اتمها. در غیراین صورت، یعنی وقتی تاثیر h قابل اغماض نباشد، اندازهگیری در حوزهی کوانتومی است. کوچکی ثابت ِپلانک h نشان میدهد که تا چه میزان اندازهگیری در محدودهی اتمها و ذرات مادون اتمها دشوار میباشد.
بهدلیل حساسیت ذرات کوانتومی نسبت به کوچکترین کنشها میباید ابزار اندازهگیری چنان انتخاب شوند که کمترین تاثیر را بر آنها داشته باشند، یعنی بسیار کوچکتر از تاثیر متقابلِ ذرات بر ابزار تا اصولا اندازهگیری معنا داشته باشد. البته، لازم است بدانیم که ما نمیتوانیم تاثیرِ ابزار بر ذراتِ کوانتومی را بطور دلخواه کوچک کنیم. برای روشن شدن این مطلب به این پرسش میپردازیم که: آیا اصولا ما شانسِ ملاحظهِ ذراتِ کوانتومی، آنگونه که واقعاً هستند، را داریم؟
ملاحظهی ذراتِ کوانتومی بهشکلی که هستند مشروط میشود به امکان تاثیرگذاری هرچه کمتر ابزار اندازهگیری بر آنها، برای مثال کوچکتر از اثر h (!؟). از آنجا که ثابت پلانک h مرز تاثیرگذاری حداقلی در اندازهگیریهای کوانتومی است (مرزِ توانِ شناختِ علمِ فیزیکِ کنونی) امکانِ اندازهگیریِ دقیقتر از اندازه اثر پلانک وجود ندارد. این گفته بهمعنای آن است که ما قادر به کسب اطلاع از دنیای مادون ثابت پلانک را نداریم و احتمالا بههمین خاطر نیز ناتوان از حل مسائلی مانند مهبانگ هستیم. یعنی، شناختِ ما از کیهان تا اثر پلانک ممکن است؛ کمیتی که مرزِ معرفتشناسی علم فیزیک حاضر را نشان میدهد. در اینجا لازم است پیش از ادامه مطلب به یک اصل، اصلِ عدمِ قطعیت، اشارهای داشته باشیم:
ما در این مقاله بحثِ اندازهگیری کمیتهای کوانتومی را مدنظر داریم. در دنیای کوانتومی، بعکس دنیای کلاسیک اندازهگیری کمیتها، مانند مکان و تکانه خطی یک ذره، متاثر از آن است که کدام یک از این کمیتها ابتدا و کدام یک بعد از آن اندازه گیری میشود ـ مسئلهای که در دنیای ماکروسکوپی با آن مواجه نیستیم. برای مثال تعیینِ اندازهِ تکانه و بعد از آن مکانِ ذره بر نتیجه مکانِ ذره اثر میگذارد و بعکس، یعنی اندازهگیری مکانِ ذره و سپس تکانهِ ذره بر نتیجه تکانهِ ذره تاثیر میگذارد. این تاثیر بهوسیله اصلِ عدمِ قطعیت (هایزنبرگ۷) تعیین میشود. در عین حال لازم است، بنابر توضیحات پیشتر، در نظر داشته باشیم که نتایج اندازهگیریها ارزشیهائی تصادفی (احتمالاتی) هستند. به این معنا که ارزشهای مربوطه پیش از اندازهگیری ناشناخته شده نیستند بلکه نامعین هستند! و این یک فرق بسیار بزرگ میان دیدگاه نظریه کوانتوم و فیزیک کلاسیک نسبت به کمیتهاست. به این معنا که در دنیای کوانتوم تا زمانیکه یک ذره را اندازهگیری نکردیم هیچ نمیدانیم که ذره دقیقا در کجاست. در واقع پیش از اندازهگیری ذره در حالتهای مختلف برهمنهی۳ است.
و حال ادامه مطلب: صرفنظر از مرز شناخت فیزیک کنونی ما، تعیین شده از جانبِ ثابتِ پلانک h، لازم و مهم است بدانیم که مسئلهی مربوط به فرایندِ اندازهگیری کوانتومی هنوز (کاملا) روشن نشده است. یعنی، ما هنوز حتی بطرز نظری دقیقا نمیدانیم که چگونه از احتمالات (کوانتومی) به ارزش اندازهگیری شده (کمیت کلاسیک) میرسیم. بیشک این گفته که ’ارزش اندازهگیری، ارزش سنجیده شده توسط دستگاه اندازهگیری است‘نمیتواندپاسخ رضایتبخشی برای مسئلهی ذکر شده ما باشد. چراکه پاسخ کافی میباید کل رخدادها میان ابژکتِ کوانتومی و ابزارِ اندازهگیری، یعنی تمامی کنش و واکنشها میان آن دو در حین اندازهگیری و پروسه شکلگیری ارزشِ معین از احتمالات کوانتومی، را شناخت. از دهه هفتاد قرنِ گذشتته تلاشِ فیزیکدانها، از جمله ایچ. دیتر زه و وُسیج ایچ. زورک، بر این است که بتوان مراحل نامبرده را با یاری مفهومِ ناهمدوسی۳ و با آن مسئله اندازهگیری کوانتومی را درک و توضیح داد. پیشرفت تکنیک و تحقیقات نظری روزافزون در سالهای اخیر در این عرصهی بنیادی برای نشان دادن و اثبات پدیدههای کوانتومی و همچنین بهرهبرداری از آنها امیدوار کننده است. اما همزمان لازم است که دستآوردهای علم فیزیک از جانب فیلسوفان طبیعی به چالش کشیده شود. این امر برای تعبیر درست از مفهومها و توسعه معرفتشناسی مدرن بسیار حائز اهمیت است. یکی از نکات قابل تامل و مهم در این رابطه درک همه جانبهی لحظه گذار از دنیای کوانتومی به دنیای کلاسیک است.
گفتیم که تغییر حالت یک جسم کوانتومی، گذر از دنیای کوانتومی به دنیای کلاسیک، ناگهانی (آنی) میباشد. اروین شرودینگر، فیزیکدان اتریشی، این تغییر ناگهانی در اندازهگیری کوانتومی را جالبترین نکتهی کل نظریه مکانیک کوانتومی میداند، لحظهی گریز از واقعگرائی ساده لوحانه.۸
اکنون سعی میکنیم با یاری توضیحات ارائه شده دو مطلب (دو مثال) ذکر نموده در ابتدای مقاله را برای آشنائی اولیه با زوایائی از پدیدهها و واقعیتهای کوانتومی در رابطه با مسئله و مفهوم اندازهگیری، بدون ارائه استدلال ریاضی، توضیح دهیم. در مورد مطلب اول گفتیم:
“برای ما تصور اینکه یک ذرهی میتواند همزمان در مکانهای مختلف باشد اگر نه محال حداقل اما بسیار دشوار است.”
و در مورد مطلب دوم، یعنی ’آزمایش دو شکاف‘ و نتیجه حاصل از آن توضیح مختصری به این شکل دادیم:
“زمانیکه ما یک ذرهی کوانتومی مانند فوتون یا الکترون را بسوی دوشکاف گسیل میداریم (تصویر۱) نتیجه، برخلاف تصور کلاسیک ما که ذره از یکی از دو شکاف خواهد گذشت، چنان است که گوئی ذره از هر دو شکاف گذشته است!”
ما، خواسته و یا نخواسته، بایستی اذعان کنیم که با تفکیک مفهوم ذره (Teilchen, particle)، مانند ذره فوتون یا الکترون متعلق به دنیای کوانتوم از مفهوم ذره در دنیای کلاسیک مشکل داریم و اغلب این دو را در یک مرتبه قرار داده و همتراز هم تلقی میکنیم. غافل از اینکه در اولی صحبت از یک تک ذره مانند الکترون است و در دومی از سیستمی (ensemble) متشکل از تعداد غیرقابل تصور از ذرات کوانتومی، برای مثال بخش کوچکی از یک سنگ ریزه بسیار ناچیز. روشن است که فقدان شناخت کافی از اختلاف میان این دو مفهوم و تفکیک آنها ازهم سبب کج فهمیها و ارزیابیهای نادرست شود. در همین ارتباط میتوان این پرسش را مطرح کرد که اجسام متشکل از صدها ذرات کوانتومی، مانند اتمهای “سنگین”، جزو کدام یک از دو بخش نامبرده محسوب میشوند؟
برای پاسخ به این نوع پرسشها میتوان از آنچه در ابتدای همین بخش آمده بهرهجست. در آنجا توضیح دادیم:
“چنانچه بتوان در اندازهگیریها ناثیر h را نادیده گرفت (h => 0) در اینصورت اندازهگیری در حوزهی کلاسیکی قرار دارد، یعنی در ابعادی بزرگتر از محدودهی اتمها. در غیراین صورت، یعنی وقتی تاثیر h قابل اغماض نباشد، اندازهگیری در حوزهی کوانتومی است.”
به این ترتیب، اتمها و ملکولها، از آنِ دنیای کوانتوم محسوب میشوند، چراکه تاثیر ثابت پلانک h در مورد این نوع اجسام غیرقابل چشم پوشی است.
ذره و موج
قابل توجه است وقتی ما در آزمایش دو شکاف بهجای مفهوم ذره از مفهوم موج استفاده کنیم ظاهرا مشکل چندانی با نتیجه آزمایش نداریم و آن را میپذیریم. یعنی، قبول میکنیم که موج میتواند همزمان از هردو شکاف بگذرد!
علت این برداشت دوگانه، دو حس متفاوت، چیست؟
موج (Welle, wave) یا آنگونه که فیزیدکدانها بیان میدارند میدان (Feld, field)، بعکس ذره، ابژکتی گسترده است که اجزایش همزمان و مستقل از هم وجود دارند. اجزاء امواج میتوانند در یک نقطه متمرکز شده و عملکرد مشترکی داشته باشند. بهنظر این یکی از ویژگیهای “ذرات” میکروسکوپی است.۹ این ویژگی امکان درک انرژیهای گسسته الکترونها در اتم هیدروژن با یاری امواج ایستاده را قابل فهم میکند.۸ آیا ذره در واقعیت همان موج (میدان، امواج) است؟ اگر چنین باشد، ذره همه جا هست و در عین حال هیججا نیست. امواج میتوانند، در صورتی که جذب نشوند، در برخورد با ابزار اندازهگیری، با ردیابها (Detektoren, dectors)، بهشکل غیردترمینیستی در مکانی غیرقابل پیشبینی، یعنی در مکانهای مختلف، بهحالت یک “بسته موج” (Wellenpaket, wave package) درآیند (این حالت را فروپاشی تابع موج مینامند۴). بهنظر “بسته موج” همان چیزی است که در ما آن حسی را ایجاد میکند که از آن به نام ذره یاد میکنیم. در واقع این تابع موج است که ویژگی ظاهر شدن در شکل “بسته موج” را دارد و به این ترتیب توصیف مفهوم ذره کوانتومی را ممکن میکند.
مراجع
1. https://de.cleanpng.com/png-wf4i0g
2. Hassan Bolouri, The Science of Thinking – Principles and Methods
حسن بلوری، علم اندیشیدن ـ ریشهها و روشها، زنجان، نشر هزارهی سوم، ۱۳۹۴
3. Hassan Bolouri, The Concept of Coherence and Decoherence
حسن بلوری، مفهوم همدوسی و ناهمدوسی، منتشر شده در سایتهای فارسی زبان، دتسامبر ۲۰۲۰
4. Hassan Bolouri, The Concept of Reality in Quantum Theory
حسن بلوری، مفهوم واقعیت در نظریه کوانتوم، منتشر شده در سایتهای فارسی زبان، اکتبر/ نوامبر ۲۰۲۰
5. Hassan Bolouri, Principle of Causality?
حسن بلوری، اصل علیت؟، منتشر شده در سایتهای فارسی زبان، ژانویه ۲۰۲۰
6. Joachim August Messer, Das Realismus-Problem der Quantenmechanik angesichts der Dekohärenz-Interpretation, Dissertation, Justus-Liebig-Universität Gießen, 2007
7. Werner Heisenberg, Der Teil und das Ganze, Gespräche im Umkreis der Atomphysik, R. Pieper Verlag, 1969; Physics and Beyond, Encounters and Conversation, Tr. by Arnold J. Pomerans, London, Allen & Unwin, 1971
ورنر هایزنبرگ، جزء و کل، ترجمه حسین معصومی همدانی، مرکز انتشارات دانشگاهی تهران، ۱۳۶۸
8. Erwin Schrödinger, Die gegenwärtige Situation der Quantenmechanik, In: Naturwissen-schaften 23, 1935
9. H. Dieter Zeh, Physik ohne Realität, Springer-Verlag, Berlin Heidelberg, 2012



